https://school.programmers.co.kr/learn/courses/30/lessons/49189
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
n개의 노드가 있는 그래프가 있습니다. 각 노드는 1부터 n까지 번호가 적혀있습니다. 1번 노드에서 가장 멀리 떨어진 노드의 갯수를 구하려고 합니다. 가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.
노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 vertex가 매개변수로 주어질 때, 1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return 하도록 solution 함수를 작성해주세요.
제한사항
- 노드의 개수 n은 2 이상 20,000 이하입니다.
- 간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
- vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.
입출력 예
| n | vertex | return |
| 6 | [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]] | 3 |
입출력 예 설명
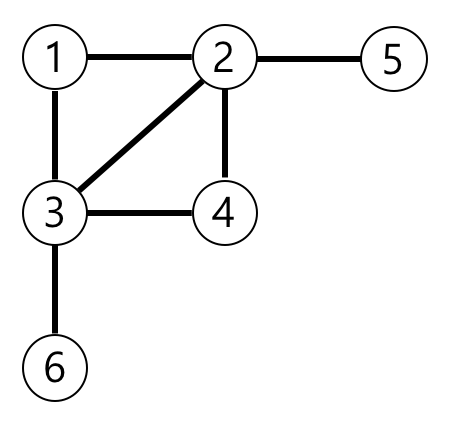
예제의 그래프를 표현하면 아래 그림과 같고, 1번 노드에서 가장 멀리 떨어진 노드는 4,5,6번 노드입니다.
구현코드
1. 시간초과 난 코드
def solution(n, edge):
answer = 0
que = [(1,0)]
visited = [0]*(n+1)
maxDistance=0
maxCounts=0
visited[1]=1
while que:
value, distance = que.pop(0)
if distance !=0 and distance > maxDistance :
maxDistance = distance
maxCounts = 1
elif distance !=0 and distance == maxDistance:
maxCounts += 1
for node in edge:
if (node[0] == value ) and (visited[node[1]] == 0 ):
que.append((node[1], distance+1))
visited[node[1]]=1
elif (node[1] == value ) and (visited[node[0]] == 0 ):
que.append((node[0], distance+1))
visited[node[0]]=1
# visited[value] = 1
return maxCounts
[시간복잡도]
1. que는 최악의 경우 n개의 노드를 모두 방문
2.while 루프 내에서 que.pop(0)을 호출하는데, 이는 리스트에서 첫 번째 요소를 제거하므로 O(n)의 시간 복잡도를 가짐
3. for 루프 내에서 edge의 모든 요소를 순회하므로 O(m)의 시간
4. while 루프의 내부에서 for 루프를 실행하므로 전체 시간 복잡도는 O(n×m)
2. 딕셔너리 활용
from collections import deque
def solution(n, edge):
answer = 0
que = deque([(1, 0)])
visited = [0] * (n + 1)
maxDistance = 0
maxCounts = 0
visited[1] = 1
my_map = {}
for i in range(1, n + 1):
my_map[i] = []
for node in edge:
my_map[node[0]].append(node[1])
my_map[node[1]].append(node[0])
while que:
value, distance = que.popleft()
if distance != 0 and distance > maxDistance:
maxDistance = distance
maxCounts = 1
elif distance != 0 and distance == maxDistance:
maxCounts += 1
for node in my_map[value]:
if visited[node] == 0:
que.append((node, distance + 1))
visited[node] = 1
return maxCounts[시간복잡도]
1. 그래프를 인접 리스트 형태로 변환하는 과정은 O(m) (m은 간선의 수)
2. while 루프는 최대 n번 반복 (n은 노드의 수)
3. while 루프 내의 for 루프는 각 노드의 이웃 노드를 순회하므로, 최악의 경우 모든 간선을 순회하게 되어 O(m)의 시간 복잡도
4. 전체 시간 복잡도는 O(n+m)
from collections import deque
def solution(n, edge):
answer = 0
graph = []
for i in range(n+1):
graph.append([])
for e in edge:
start, end = e
graph[start].append(end)
graph[end].append(start)
que = deque([])
visited = [False]*(n+1)
distances = [0]*(n+1)
que.append((1,0))
visited[1] = True
while que:
vertex, distance = que.popleft()
distances[vertex] = distance
for neighbor in graph[vertex]:
if not visited[neighbor]:
visited[neighbor] = True
que.append((neighbor, distance+1))
for distance in distances:
if distance == max(distances):
answer+=1
return answer'Algorithm(Python)' 카테고리의 다른 글
| [Python] 프로그래머스 - 미로탈출 (bfs) (2) | 2023.10.10 |
|---|---|
| [Python] k번째수 - 프로그래머스 (0) | 2023.08.31 |
| [Python] 최소직사각형 - 프로그래머스 (0) | 2023.08.31 |
| [Python] 달리기 경주 (0) | 2023.08.24 |
| [Python] 없는 숫자 더하기 (0) | 2023.08.24 |



